INTRODUCCIÓN AL TEOREMA DE DE GÖDEL · [DESDE CERO] 12.0 💡 [ INTERESANTE ! ] YouTube

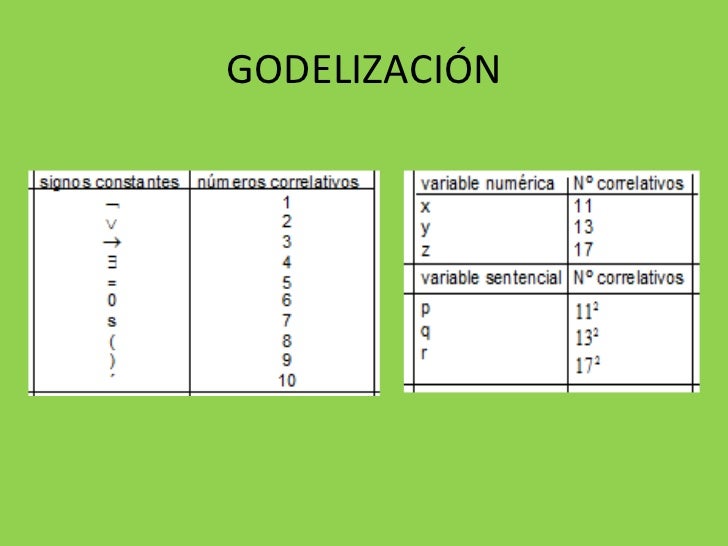
Gödel nos descubrió que la verdad es una categoría superior a la demostrabilidad. Y, por otra parte, el teorema de Gödel sólo se aplica a sistemas deductivos del tipo que se utiliza en matemáticas. Nos demuestra que el sistema matemático más perfecto que podamos conseguir, con un número finito de axiomas y reglas de inferencia, es.. La demostración de este teorema pasa por construir una cierta fórmula, la «sentencia de Gödel» G, que no puede ser probada ni refutada en la teoría aritmética recursiva T: ni G ni ¬G (la negación de G) son teoremas de T.Se dice entonces que G y ¬G son indecidibles o independientes en T.. Para llegar a esta, Gödel desarrolló un método para codificar signos y fórmulas mediante.

El Teorema de de Gödel

Teorema Da De Godel

EL TEOREMA DE DE GÖDEL MATEMÁTICAS EN TRES MINUTOS YouTube

(PDF) EL TEOREMA DE GöDEL, LA MATEMATICA Y EN PSICOLOGIA

Los teoremas De De Kurt GöDel

Teorema de de Gödel YouTube

Teorema de de Gödel PDF Axioma Lógica de primer orden

Teoremas y filosofía de la de Kurt Gödel

Los teoremas De De Kurt GöDel

TEOREMA DE DE GÖDEL

PPT Teoremas de Completitud e de Gödel PowerPoint Presentation ID6570182

Questões Cosmológicas

Teoremas de de Gödel PDF Axioma Prueba matemática

Teorema de de Gödel para Filósofos PDF

Teorema de de Gödel YouTube

Teoremas de de Gödel PDF Axioma Prueba matemática

[PDF] GÖDEL Los Teoremas De La Intuición Tiene Su Lógica Gustavo Ernesto Piñeiro

Los teoremas De De Kurt GöDel

INTRODUCCIÓN AL TEOREMA DE DE GÖDEL · [DESDE CERO] 12.0 💡 [ INTERESANTE ! ] YouTube

Teorema de de Gödel aplicado a la industria del software Distillery

Gödel combina los axiomas de los Principia con los Axiomas de Peano. Toda la demostración de los Teoremas de Incompletitud es aplicable a cualquier sistema que permita decidir la veracidad de una relación definida de forma recursiva primitiva, es decir, en un número finito de pasos. Esto incluye también la Teoría de Conjuntos de Zermel.. Gödel también esbozó un segundo teorema de incompletitud igualmente significativo. A lo largo de este seminario investigaremos cómo se establecen dichos teoremas, y por qué son relevantes. El texto de cabecera será el libro An Introduction to Gödel’s Theorems (Second Edition) de Peter Smith. Dicho libro