One-dimensional advection. ¶. Solve the linear advection equation: qt + uqx = 0. q t + u q x = 0. Here q is the density of some conserved quantity and u is the velocity. The initial condition is a Gaussian and the boundary conditions are periodic. The final solution is identical to the initial data because the wave has crossed the domain.. Mathematically, we’ll start with our two equations: (1) The diffusion equation without heat production and (2) the advection equation, then combine them. In steady state, we can ignore the transient term ∂T/∂t ∂ T / ∂ t, so. Another way to write the previous equation is. In this case, we can make some substitutions and find something.

1D 2D And 3D Advection And Diffusion Equations

Infinite Square Well (1D) Boundary Conditions (part 3 of 3) YouTube
![[PDF] Numerical Solution of Onedimensional Advectiondiffusion](https://d3i71xaburhd42.cloudfront.net/8c4ccd53af606ee7af4385551d79c39735ef3753/7-Figure3-1.png)
[PDF] Numerical Solution of Onedimensional Advectiondiffusion Equation Using Simultaneously
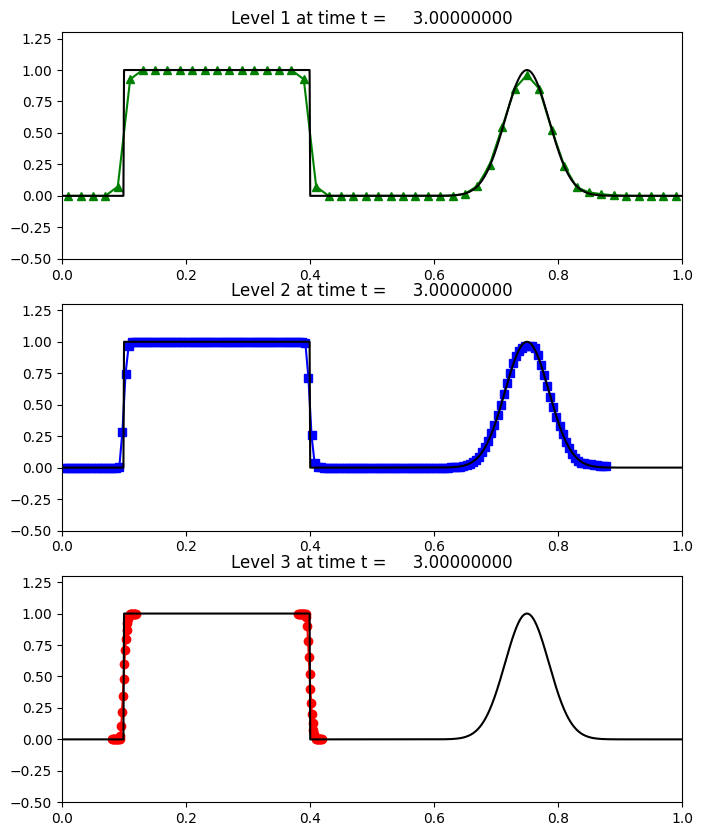
Plots
35 Drop profile shown for the second advection case (dense drop… Download Scientific Diagram
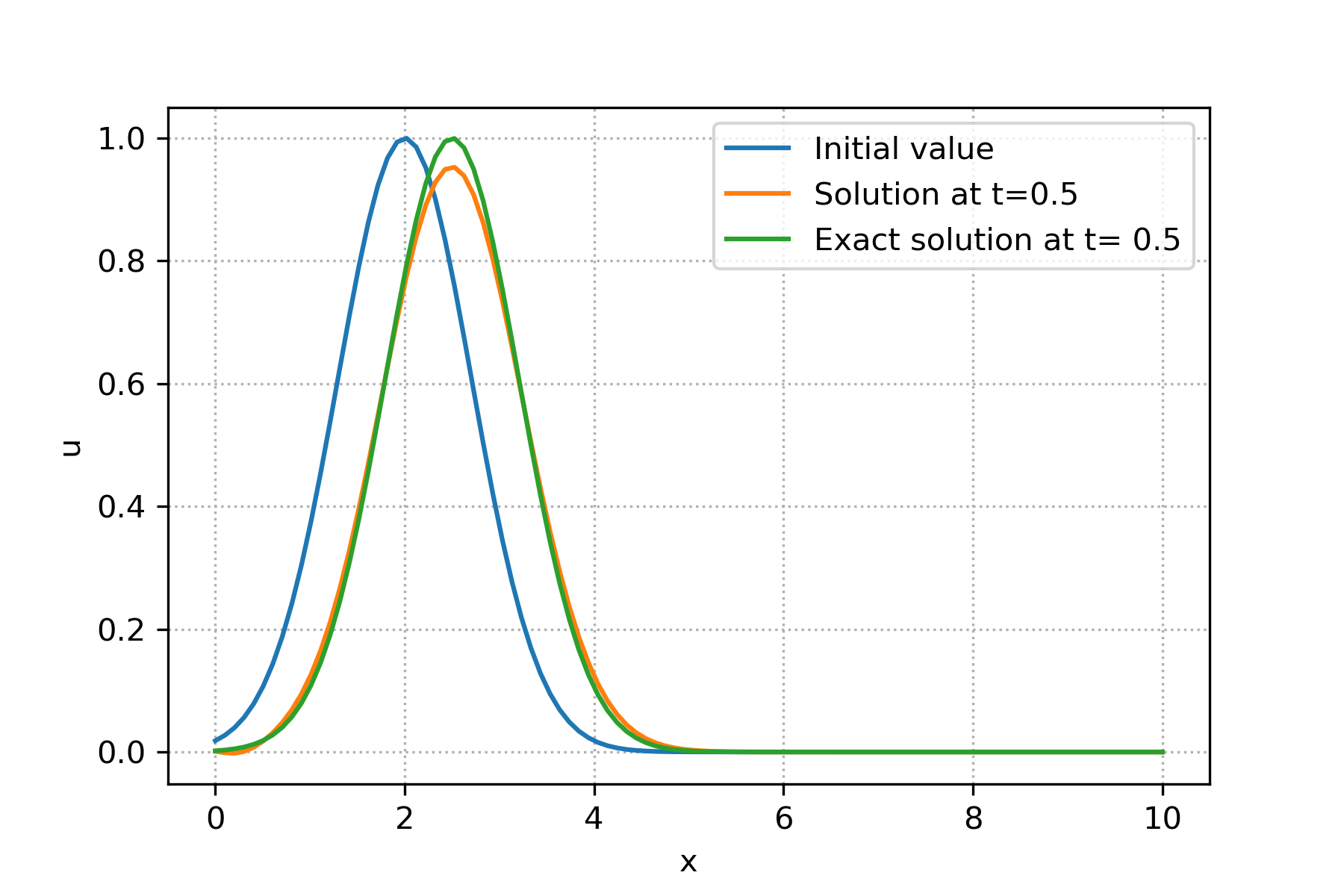
Linear 1D Advection Equation — Diff. Academy 0.0.1 documentation
![[PDF] Numerical Solution of Onedimensional Advectiondiffusion](https://d3i71xaburhd42.cloudfront.net/8c4ccd53af606ee7af4385551d79c39735ef3753/6-Figure2-1.png)
[PDF] Numerical Solution of Onedimensional Advectiondiffusion Equation Using Simultaneously

Solved 2 AdvectionDiffusion Equation The 1D
![[PDF] Numerical Solution of the 1D](https://d3i71xaburhd42.cloudfront.net/70d9e1ab58e365151eb9754df228f3e451bd32f1/11-Figure5-1.png)
[PDF] Numerical Solution of the 1D AdvectionDiffusion Equation Using Standard and Nonstandard

Pseudo twodimensional system with a square wave traveling with the… Download Scientific Diagram
Matlab Code For 1d Advection Diffusion Equation Tessshebaylo

1D AdvectionDiffusion MATLAB Simulation FTCS Scheme YouTube
For one example of the advection of a square wave (a) original… Download Scientific Diagram
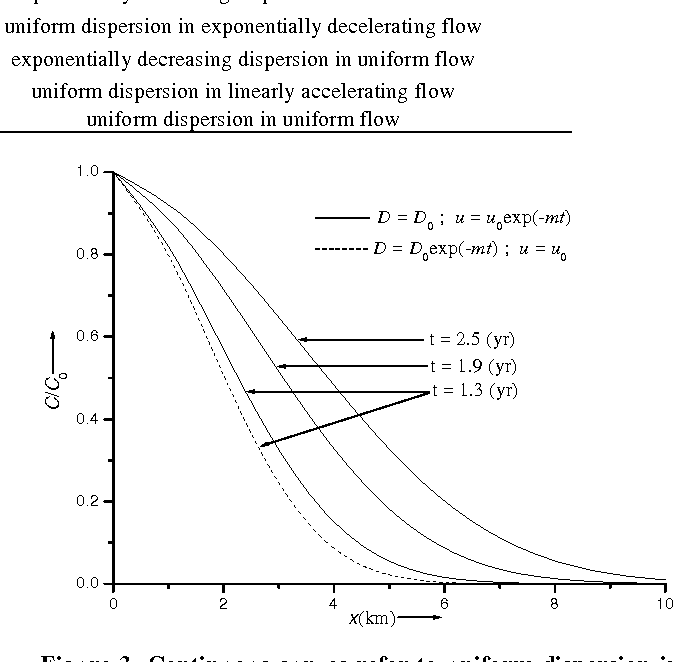
Figure 3 from Analytical Solution to the OneDimensional AdvectionDiffusion Equation with
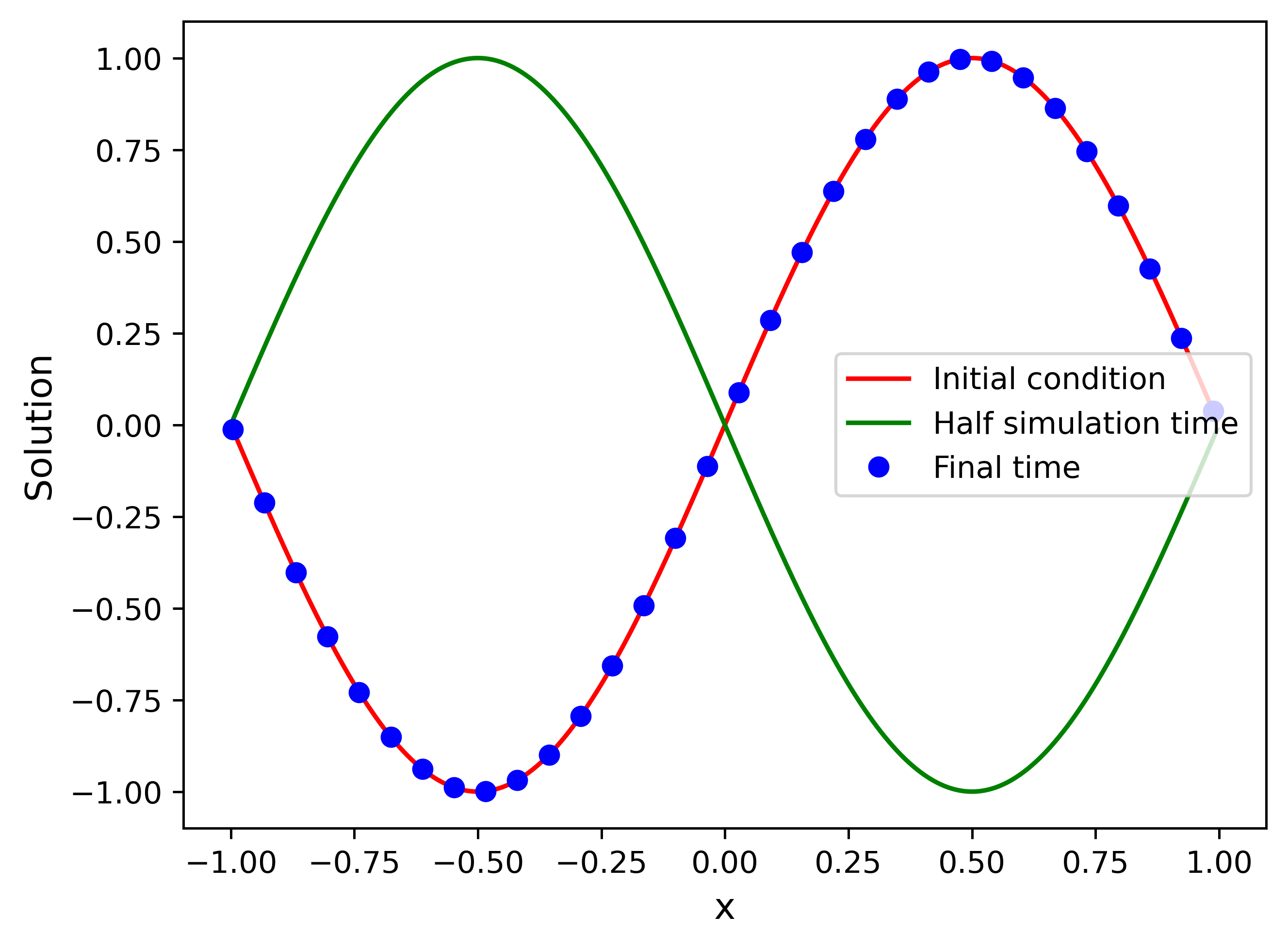
1D Linear Advection pressiodemoapps v0.14.0
1D linear advection of four shapes in a nonuniform grid using… Download Scientific Diagram
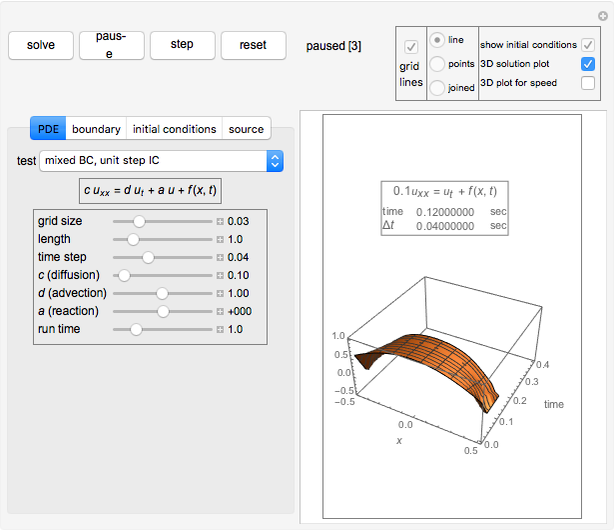
Solving the DiffusionAdvectionReaction Equation in 1D Using Finite Differences Wolfram

Solve 1D AdvectionDiffusion problem using FTCS Finite Difference Method YouTube
Numerical results for solving the advection equation. Left Unit square… Download Scientific

Dynamical states and their transitions in the active fluid model… Download Scientific Diagram
AbstractAnalytical solutions of one-dimensional (1D) advection-diffusion equations (ADE) are obtained subject to an initially pollutant-free domain and varying pulse-type input conditions.. Dispersion being proportional to square of velocity.” J. Hydrol. Eng., 16(3), 228-238. Crossref. Google Scholar. Lin, S. H. (1977). “Nonlinear.. I would like to set up fipy to solve the 1D diffusion-advection equation with sinousoidal boundary. I ended up with the following code: from fipy import * import numpy as np import matplotlib.pylab as plt def boundary(t): return 1 + 0.1 * np.sin(6*np.pi*t) nx = 50 dx = 1./nx mesh = Grid1D(nx=nx, dx=dx) n_model = CellVariable(name=”density”,mesh=mesh,value=1., hasOld=True) D_model.




