円の面積を求める公式は、面積=半径×半径×3.14(円周率)で表されます。文字式ではS = πr^2 となります。このページでは、円の面積の求め方を、計算問題と共に説明しています。また、公式の導き方のイメージも説明しています。. 円の方程式の求め方・公式|まとめ. いかがでしたか? 今回は円の方程式を扱いましたが、数Ⅲで出てくる「楕円」や「双曲線」の方程式を求める際にもこの解き方が使えます。 ぜひパターンを覚えた上で、たくさんの問題で実践してみてくださいね!
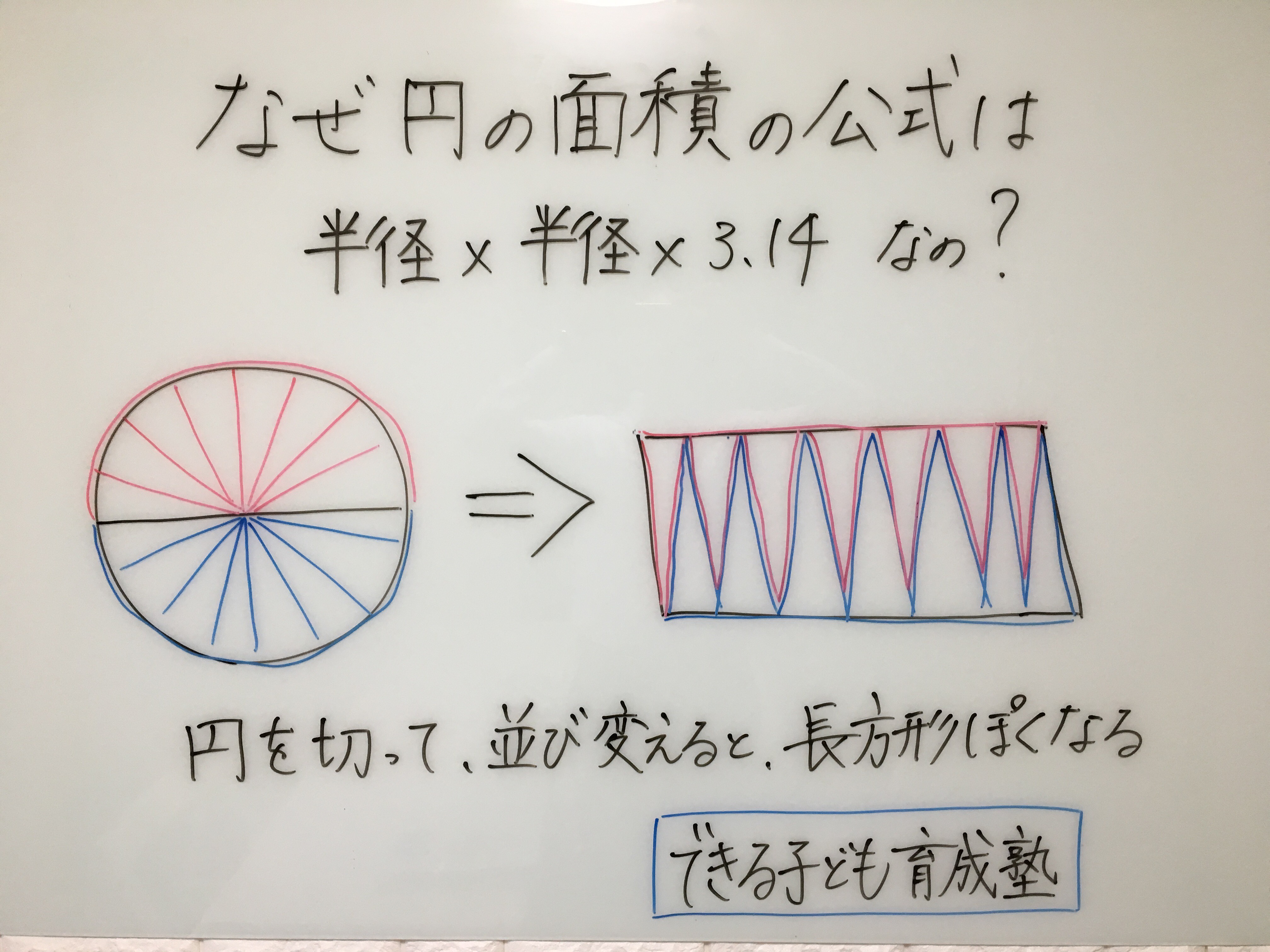
円の面積の求め方(公式)の理由を小学生に教える方法
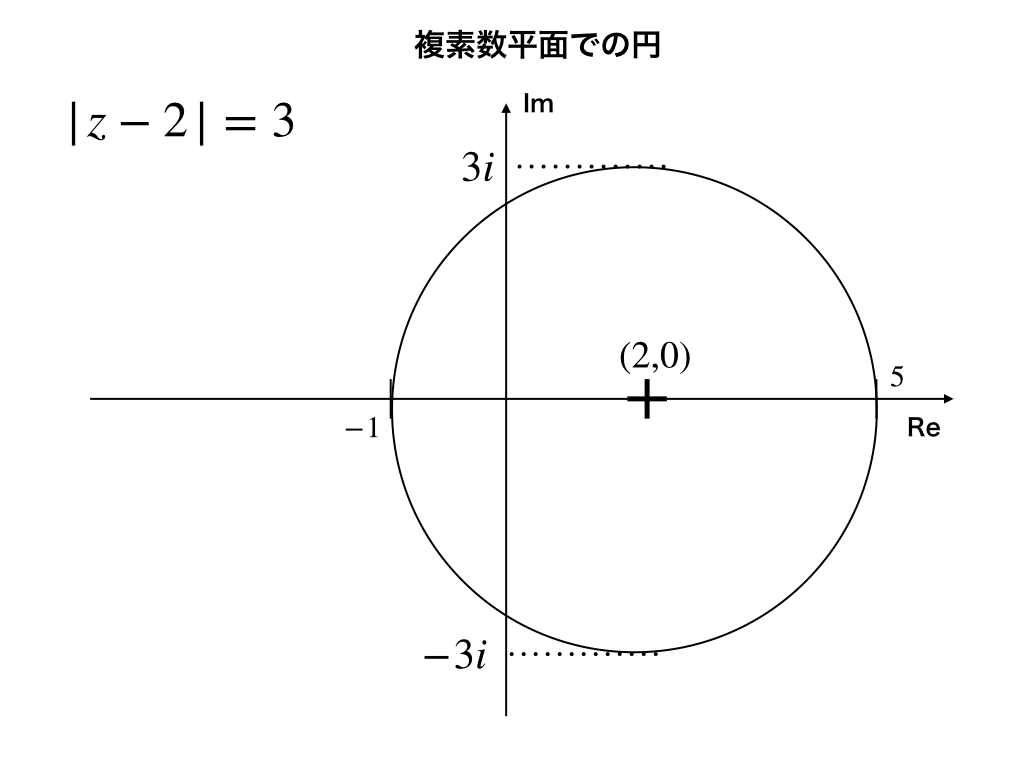
円の方程式と直線が切り取る弦の長さをわかりやすく解説!
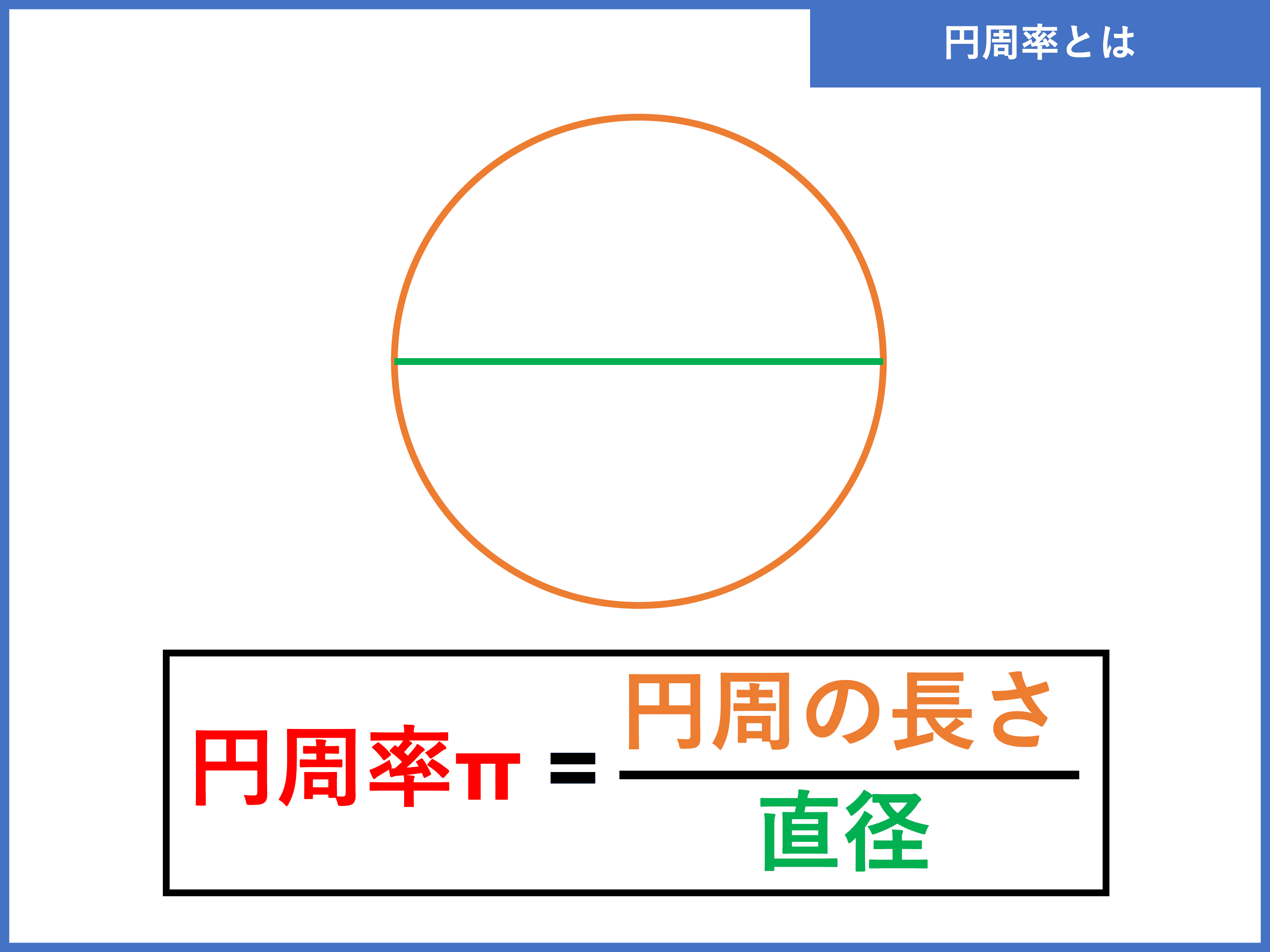
円周率 π とは?求め方や100桁までの覚え方を紹介! 受験辞典

5年生~6年生 円の面積・円周の求め方と問題たっぷり ガルボズラボ
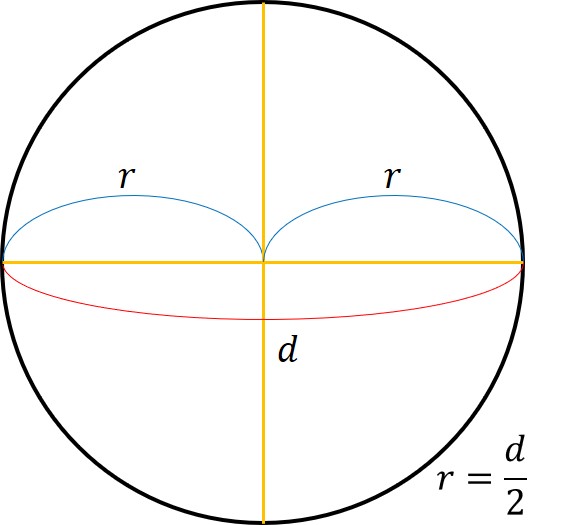
円の面積を求める公式(計算問題の解き方)
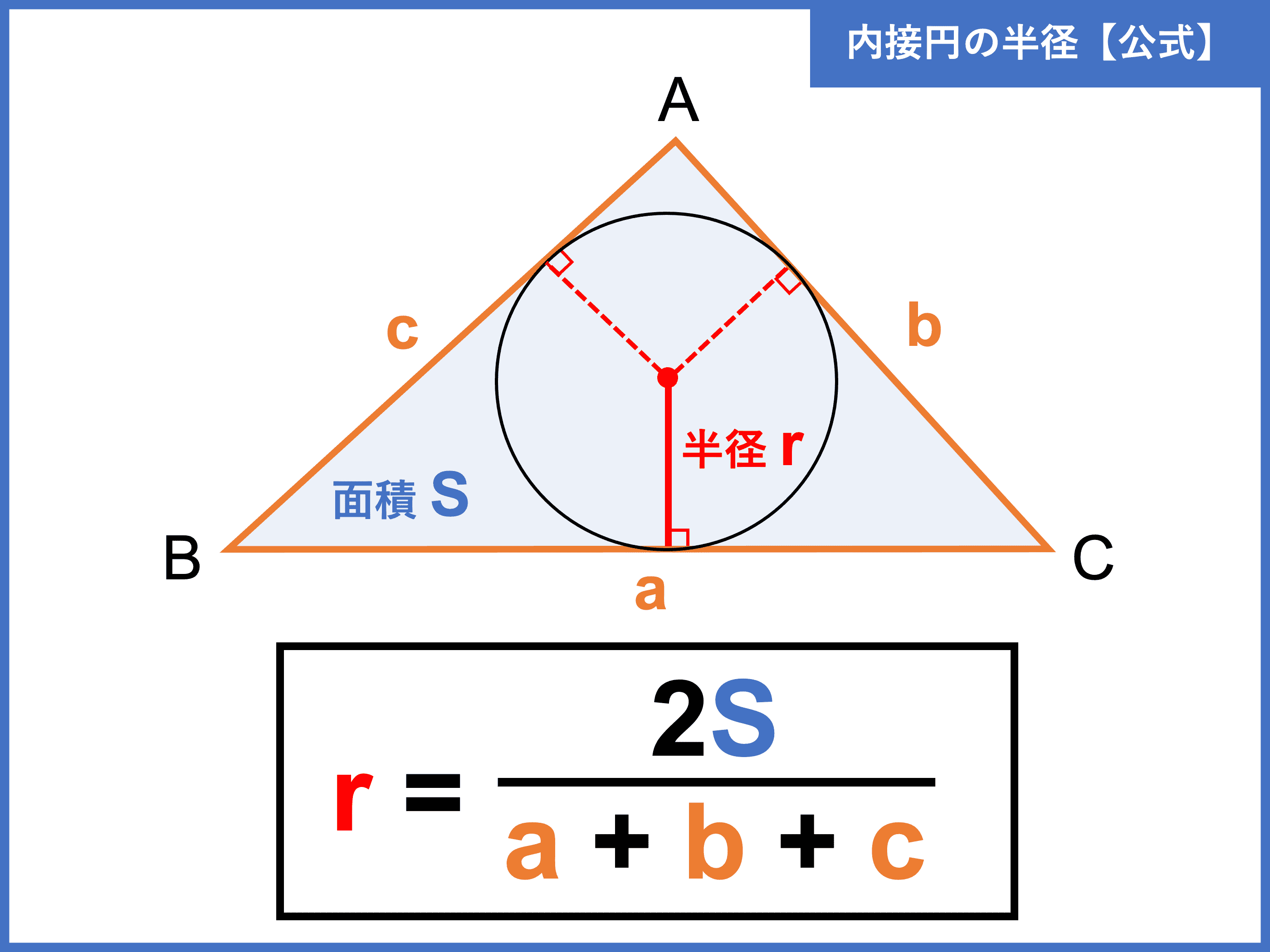
内接円とは?半径の公式や求め方、性質をわかりやすく解説! 受験辞典

内接円の半径の求め方!楽に求める時間の節約術とは?|高校生向け受験応援メディア「受験のミカタ」
![[B!] 円の面積の公式!円周の求め方と間違えないようにしよう! 中学や高校の数学の計算問題](https://cdn-ak.f.st-hatena.com/images/fotolife/y/yakunitatuzyouhou/20180528/20180528132744.png)
[B!] 円の面積の公式!円周の求め方と間違えないようにしよう! 中学や高校の数学の計算問題
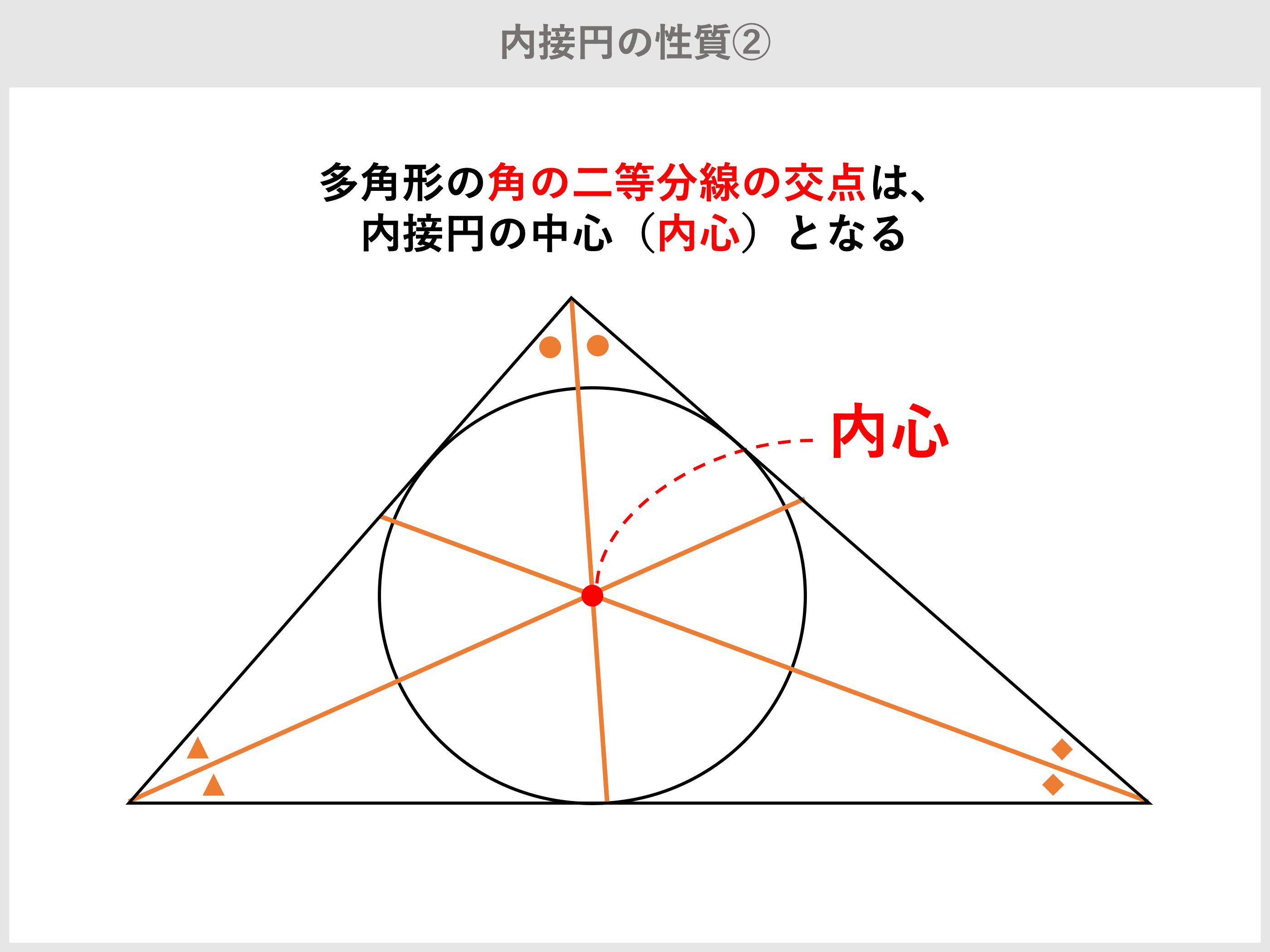
内接円とは?内接円の半径の公式や求め方、性質、書き方 受験辞典
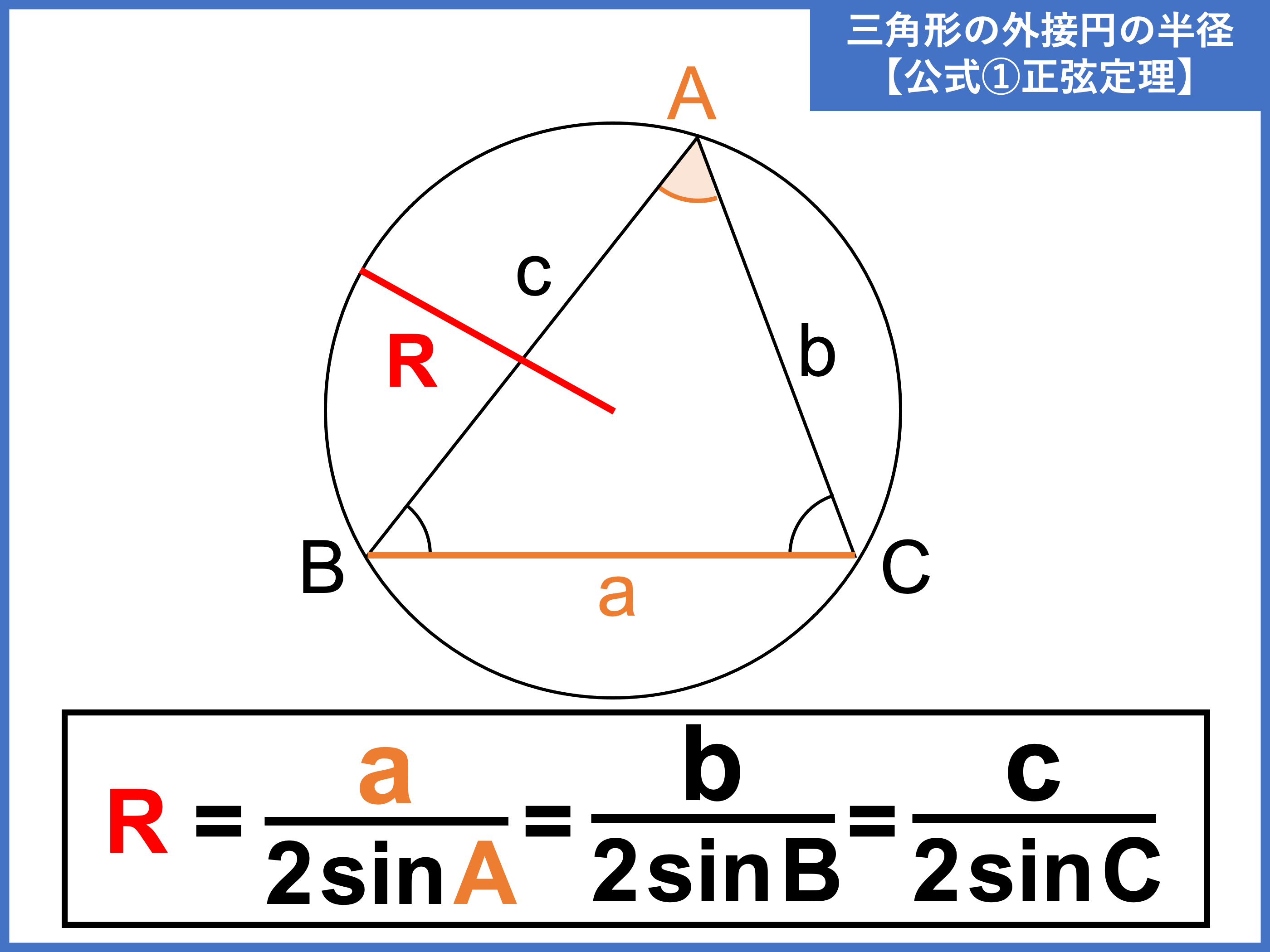
外接円とは?半径の公式や求め方、性質をわかりやすく解説! 受験辞典
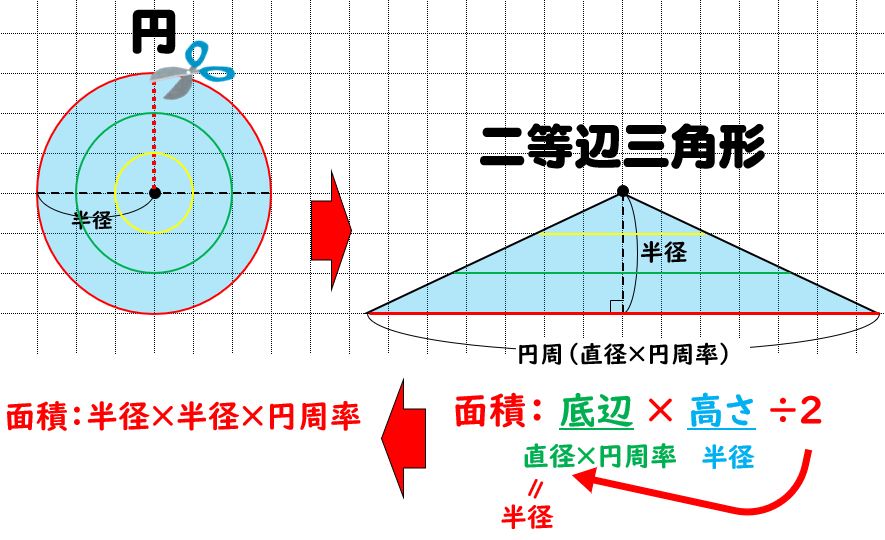
円の面積の公式|「なぜ半径と円周率で求められるのか」を小学生に分かりやすく説明する方法|数学FUN

外接円の半径の求め方がイラストで誰でも即わかる!練習問題付き|高校生向け受験応援メディア「受験のミカタ」

小6_円_円の求積(日本語版) YouTube
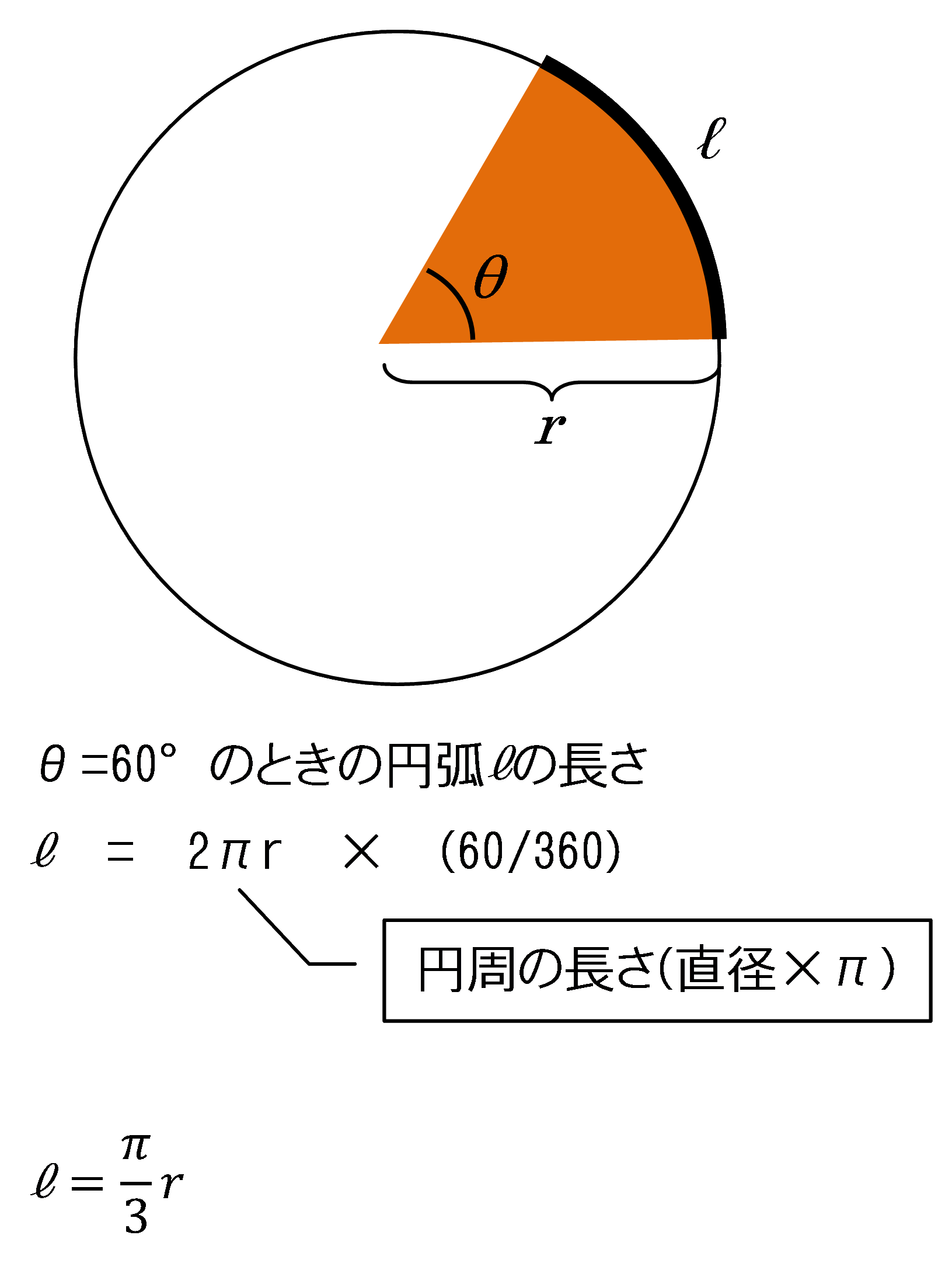
円運動:物理学解体新書
![[B!] 円周の求め方!公式は直径を使うので、半径と間違えないように! 中学や高校の数学の計算問題](https://cdn-ak.f.st-hatena.com/images/fotolife/y/yakunitatuzyouhou/20180528/20180528011158.png)
[B!] 円周の求め方!公式は直径を使うので、半径と間違えないように! 中学や高校の数学の計算問題
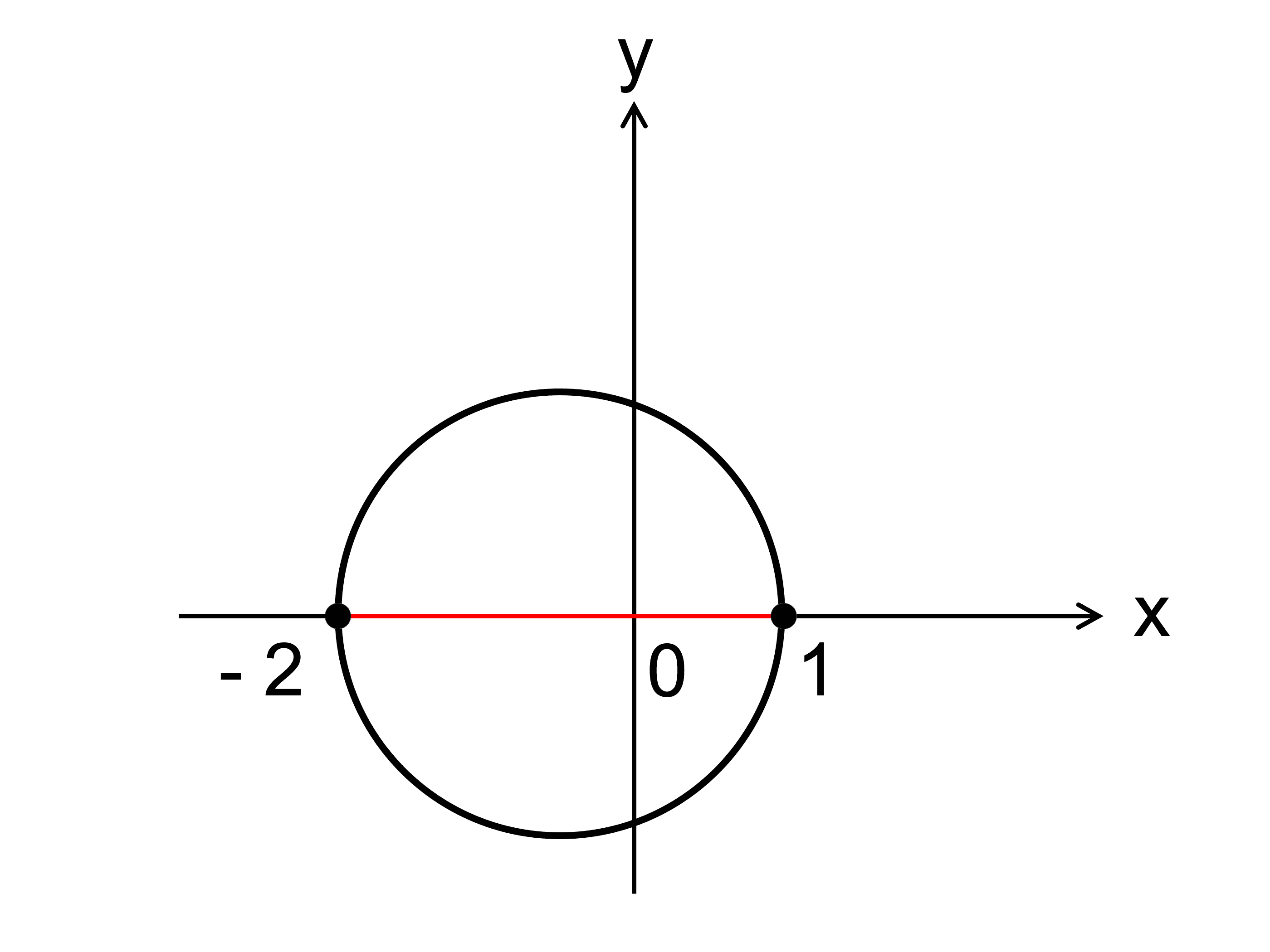
円の方程式の公式や求め方をわかりやすく解説!円の接線も 受験辞典
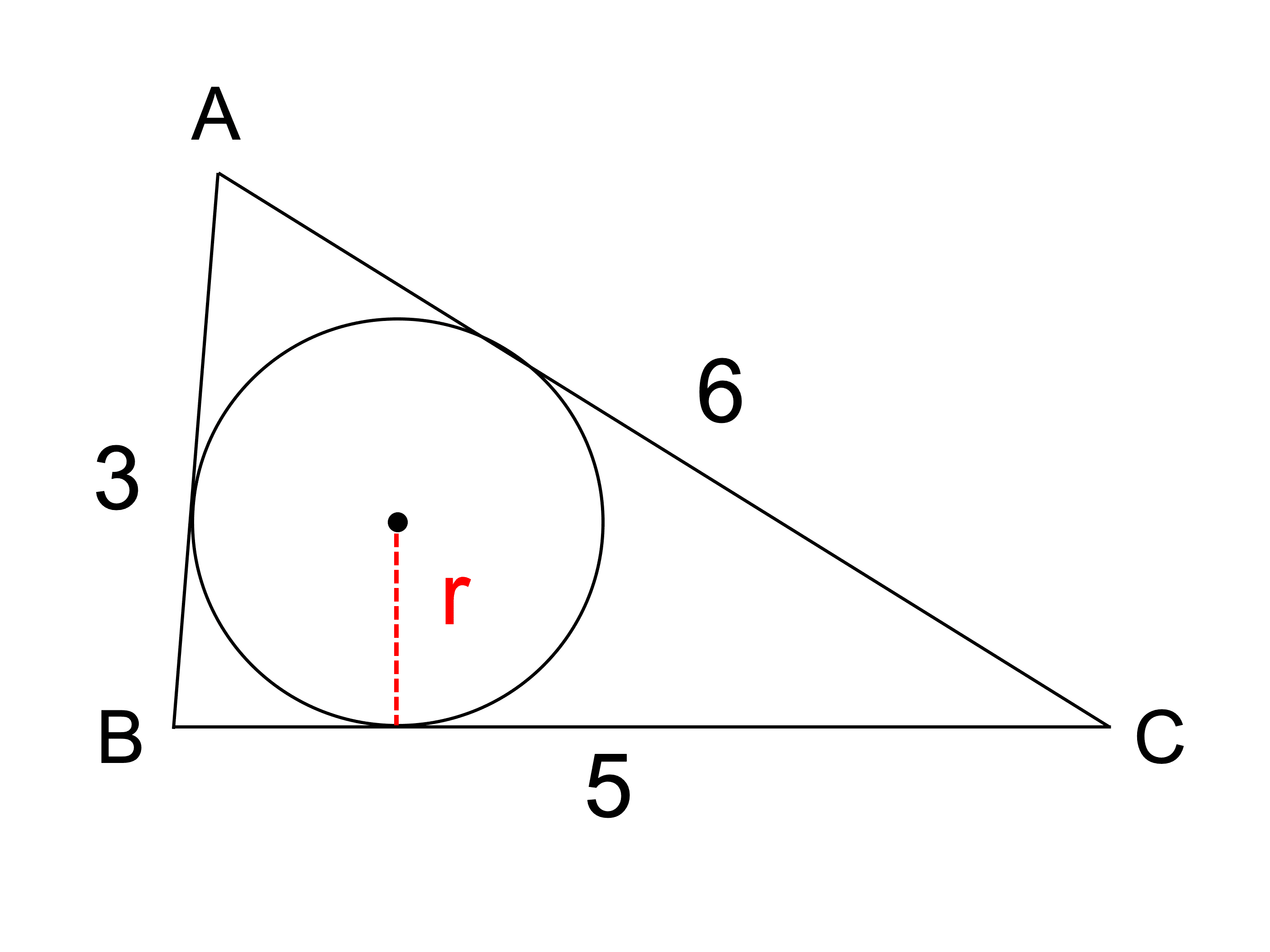
内接円とは?半径の公式や求め方、性質をわかりやすく解説! 受験辞典
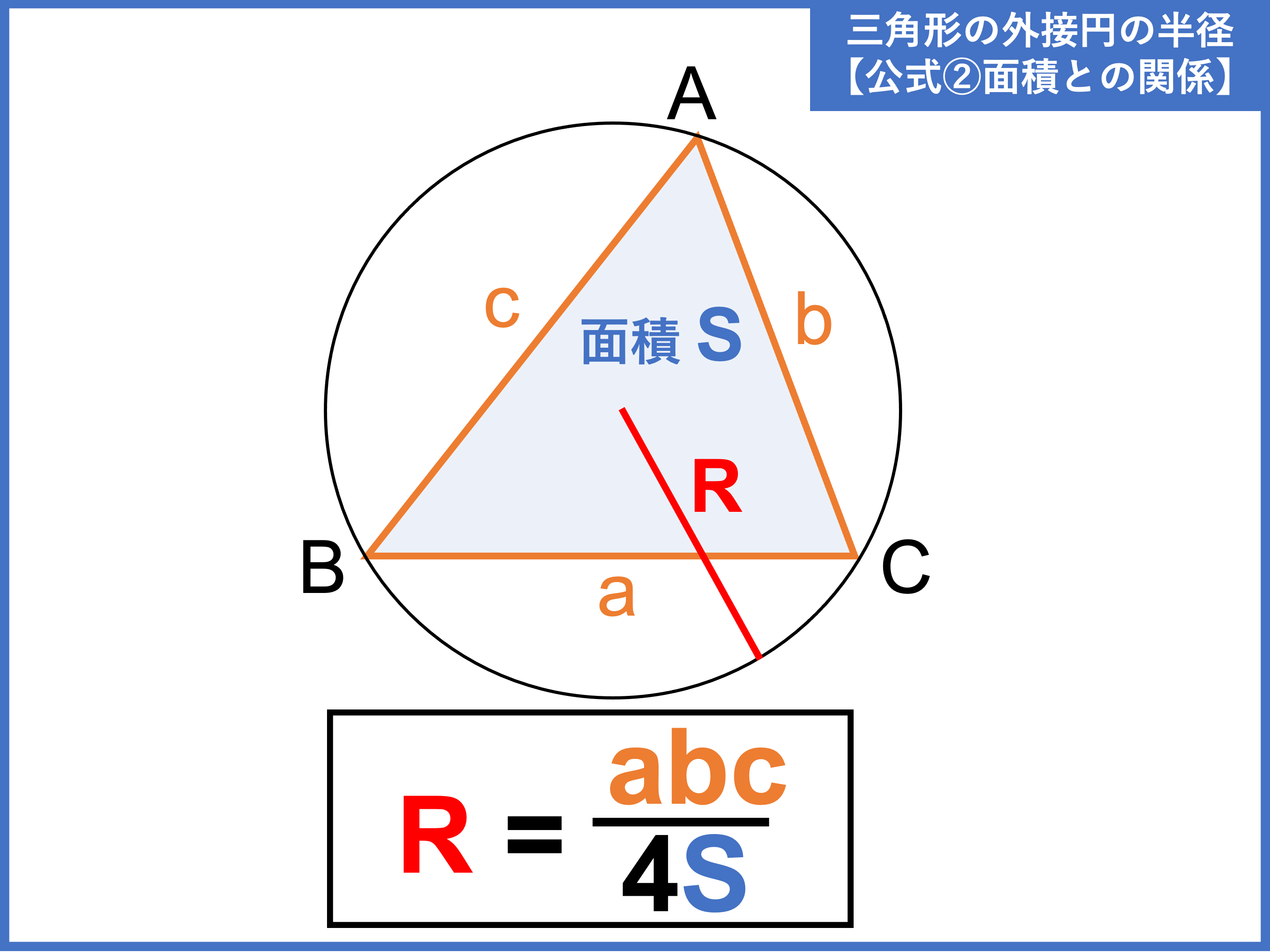
外接円とは?半径の公式や求め方、性質をわかりやすく解説! 受験辞典

「公式が覚えられない」を解消!円とおうぎ形の周りの長さ、面積の求め方 中学受験ナビ
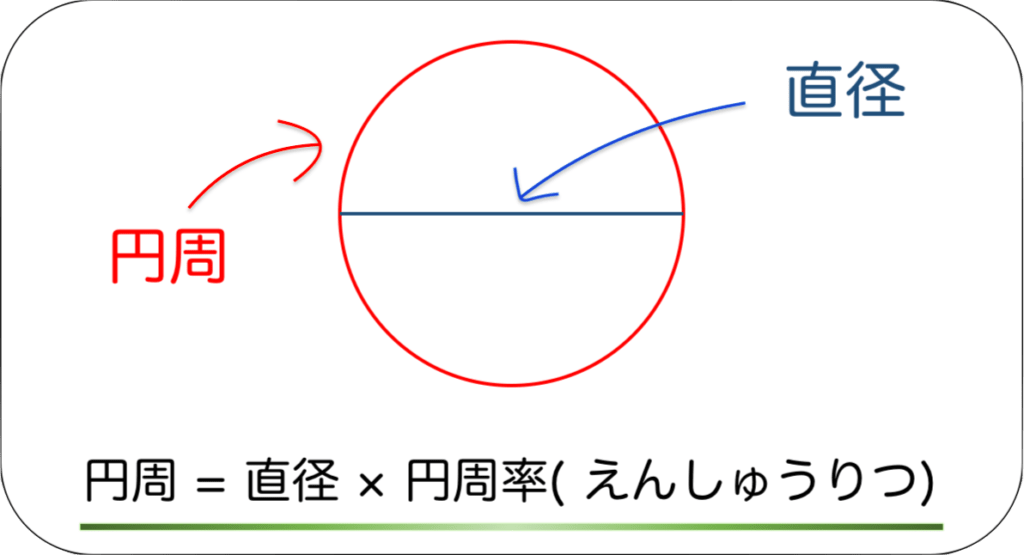
【5分でわかる】円周の求め方の公式、計算例を京大生がイラスト付きで説明します 人が右なら 私は左
円の面積の求め方【公式】 円の面積を求めるときには次の公式を使います。 円の面積=半径×半径×円周率 (円周率は小学校ではふつう3.14を、中学の数学ではΠ(パイ)を使います。) スポンサードリンク 円の面積・円周の長さを求める問題. 円の方程式:基本形・一般形の公式と中心、半径の求め方. 特定の図形を表すとき、方程式を作れるようになる必要があります。. 直線の方程式であれば、 y = ax + b を利用します。. それでは、円の方程式はどのように表せばいいのでしょうか。. 円の方程式.